math456.com - Create or Download High Quality Mathematics or Maths or Math Review or Assessment or Test Paper or Papers for Singapore Primary Schools (First Grade, Second Grade, Third Grade, Fourth Grade, Fifth Grade and Sixth Grade (PSLE)), Online Learning, Top Primary Schools' Mathematics Assessment Books, Gifted Education Program (GEP) and IQ Tests

No. 13 of 2005 PSLE Mathematics examination:

The figure below shows a rectangle 15 cm by 6 cm.
The area of Triangle A is 4 cm² and the area of Triangle B is 16 cm².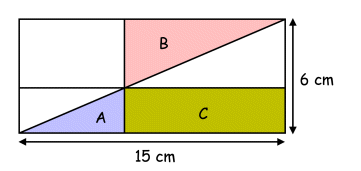

What is the area of Rectangle C?
(1) 20 cm²
(2) 22 cm²
(3) 25 cm²
(4) 28 cm²

Most pupils gave the following answer and why this answer is incorrect: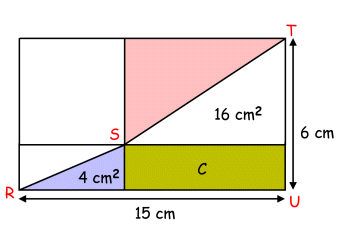

Area of triangle RTU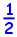
=

× 15 × 6
= 45 cm²

Area of Rectangle C = 45 - 4 - 16 = 25 cm²

The above calculation is correct provided RST is a straight line. If RST is not a straight line, then the above calculation is incorrect. We have redrawn the figure a little larger to show why this method is incorrect if RST is not a straight line.
Scroll the page down to see why RST cannot be a straight line with the information given. In other words, the figure is incorrect. Most pupils gave the 'correct' answer of 25 cm² based on the incorrect figure. If you start with an incorrect figure, you are not going to get a correct answer.

To show why all the 4 answers given cannot be correct (this method does NOT make any assumption whether RST is a straight line or not, in other words, this method works whether RST is a straight line or not):

Area of the whole rectangle = 6 × 15 = 90 cm²

Area of pink rectangle
= 2 × Area of Triangle B
= 2 × 16
= 32 cm²

Area of blue rectangle
= 2 × Area of Triangle A
= 2 × 4
= 8 cm²

C + D = 90 - 8 - 32 = 50 cm²

Using ratio,
D : 8 = 32 : C
or
D ÷ 8 = 32 ÷ C

Since this is a multiple choice question, we can use the 4 answers given to check for the correct one:

(1) C = 20, D = 50 - 20 = 30
D ÷ 8 = 30 ÷ 8 = 3.75
32 ÷ C = 32 ÷ 20 = 1.6
3.75 and 1.6 are not the same,
C = 20 cannot be the correct answer.

(2) C = 22, D = 50 - 22 = 28
D ÷ 8 = 28 ÷ 8 = 3.5
32 ÷ C = 32 ÷ 22 = 1.45 (correct to 2 decimal places)
3.5 and 1.45 are not the same,
C = 22 cannot be the correct answer.

(3) C = 25, D = 50 - 25 = 25
D ÷ 8 = 25 ÷ 8 = 3.125
32 ÷ C = 32 ÷ 25 = 1.28
3.125 and 1.28 are not the same,
C = 25 cannot be the correct answer.

(4) C = 28, D = 50 - 28 = 22
D ÷ 8 = 22 ÷ 8 = 2.75
32 ÷ C = 32 ÷ 28 = 1.14 (correct to 2 decimal places)
2.75 and 1.14 are not the same,
C = 28 cannot be the correct answer.

How to find the correct answers using Secondary school algebraic method (this method does NOT make any assumption whether RST is a straight line or not, in other words, this method works whether RST is a straight line or not):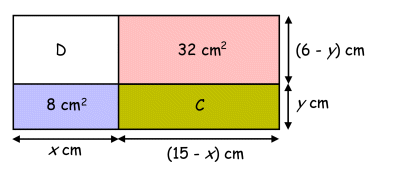

x y = 8 --- (i)

C + D = 50
(15 - x) y + (6 - y) x = 50
15y -xy + 6x -xy = 50
15y - 8 + 6x - 8 = 50 (because x y = 8)
15y + 6x = 66
5y + 2x = 22 --- (ii)

5(8/x) + 2x = 22 (because y = 8/x)
40/x + 2x = 22
40 + 2x² = 22x
20 + x² = 11x
x² - 11x + 20 = 0

This quadratic equation can be solved as follows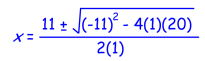

to give x = 8.70156 or x = 2.29844.

For x = 8.70156, the correct figure looks like this: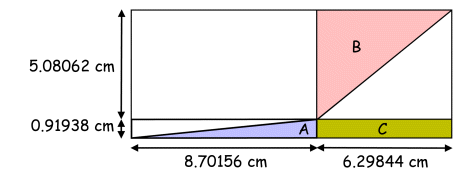

Check the answer (using calculator):
C = 0.91938 × 6.29844 = 5.79
D = 50 - 5.79 = 44.21
D ÷ 8 = 44.21 ÷ 8 = 5.53
32 ÷ C = 32 ÷ 5.79 = 5.53
C = 5.79 is a correct answer.

Note that 5.08062 ÷ 0.91938 = 0.53

For x = 2.29844, the correct figure looks like this: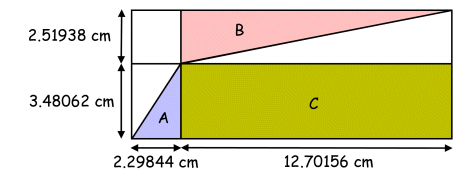

Check the answer (using calculator):
C = 3.48062 × 12.70156 = 44.21
D = 50 - 44.21 = 5.79
D ÷ 8 = 5.79 ÷ 8 = 0.72
32 ÷ C = 32 ÷ 44.21 = 0.72
C = 44.21 is also a correct answer.

Note that 2.51938 ÷ 3.48062 = 0.72

Summary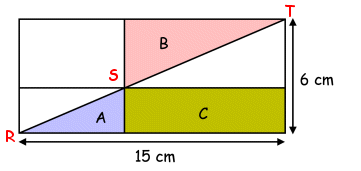

The question is correct.
The 4 given answers are incorrect.
The figure is incorrectly drawn.

The question is mathematically correct because the question did not state that RST is a straight line although the figure appears to be so. The 2 answers that we obtained (without assuming RST is straight or not) show that with the given information, RST is in fact not a straight line. The figure given in the PSLE exam shows that RST is a straight line and this is incorrect.

If RST is not a straight line, the best method for Primary school pupils is probably the trial-and-error method but it won't be easy for this question because the answer is not a whole number. We believe the designer of this question wanted RST to be a straight line and the method of solving will then be simple and will not need to involve Secondary school algebra. If the area of Triangle A, area of Triangle B, length and breadth of the big rectangle are chosen appropriately, RST can be a straight line (see the second problem below).

Three similar problems for you to try. P4 , P5 and P6 pupils should be able to do all the three problems:
Click the figure to try out a similar question from our Chili book:

Click the figure to try out a question similar in idea:

Click the figure to try out another question similar in idea:
Please send your comments to to tanbm@math456.com (B. M. Tan)

Last Updated: